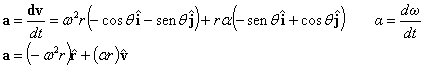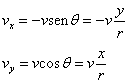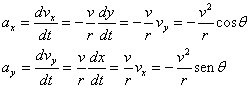El efecto Coriolis, descrito en 1835 por el científico francés Gaspard-Gustave Coriolis, es el efecto que se observa en un sistema de referencia en rotación (y por tanto no inercial) cuando un cuerpo se encuentra en movimiento respecto de dicho sistema de referencia. Este efecto consiste en la existencia de una aceleración relativa del cuerpo en dicho el sistema en rotación. Esta aceleración es siempre perpendicular al eje de rotación del sistema y a la velocidad del cuerpo.
El efecto Coriolis hace que un objeto que se mueve sobre el radio de un disco en rotación tienda a acelerarse con respecto a ese disco según si el movimiento es hacia el eje de giro o alejándose de éste. Por el mismo principio, en el caso de una esfera en rotación, el movimiento de un objeto sobre los meridianos también presenta este efecto, ya que dicho movimiento reduce o incrementa la distancia respecto al eje de giro de la esfera.
Debido a que el objeto sufre una aceleración desde el punto de vista del observador en rotación, es como si para éste existiera una fuerza sobre el objeto que lo acelera. A esta fuerza se la llama fuerza de Coriolis, y no es una fuerza real en el sentido de que no hay nada que la produzca. Se trata pues de una fuerza inercial o ficticia, que se introduce para explicar, desde el punto de vista del sistema en rotación, la aceleración del cuerpo, cuyo origen está en realidad, en el hecho de que el sistema de observación está rotando.
Un ejemplo canónico de efecto Coriolis es el experimento imaginario en el que disparamos un obús desde el Ecuador en dirección norte. El cañón está girando con la tierra hacia el este y, por tanto, imprime al obús esa velocidad (además de la velocidad hacia adelante de la carga de impulsión). Al viajar el obús hacia el norte, sobrevuela puntos de la tierra cuya velocidad líneal hacia el este va disminuyendo con la latitud creciente. La inercia del obús hacia el este hace que su velocidad angular aumente y que, por tanto, adelante a los puntos que sobrevuela. Si el vuelo es suficientemente largo, el obús caerá en un meridiano situado al este de aquél desde el cual se disparó, a pesar de que la dirección del disparo fue exactamente hacia el norte. Análogamente, una masa de aire que se desplace hacia el este sobre el ecuador aumentará su velocidad de giro con respecto al suelo en caso de que su latitud disminuya. Finalmente, el efecto Coriolis, al actuar sobre masas de aire (o agua) en latitudes intermedias, induce un giro al desviar hacia el este o hacia el oeste las partes de esa masa que ganen o pierdan latitud de forma parecida a como gira la bolita del ejemplo.

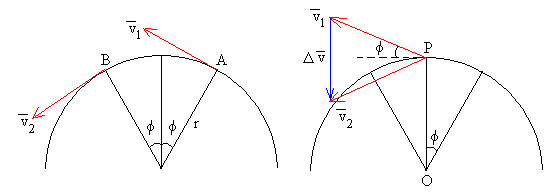
Una bolita se mueve sin fricción sobre un plato de sección parabólica que está girando a velocidad constante. La gravedad tira de la bolita hacia el centro con una fuerza directamente proporcional a la distancia respecto a éste. La fuerza centrífuga (o, mejor dicho, la ausencia de fuerza centrípeta) tira de la bolita hacia afuera. La conservación del momento angular cambia la velocidad angular de la bolita cuando ésta se mueve hacia dentro (acelera) y hacia afuera (frena). También puede expresarse diciendo que, para mantener su velocidad líneal, la bolita cambia su velocidad angular al variar la distancia respecto al eje. En cualquier caso, la magnitud subyacente es la inercia y la desviación que sufre la bolita con respecto a la dirección de los radios es el efecto Coriolis. Izquierda: El movimiento observado desde un punto de vista externo. Derecha: El movimiento visto desde un punto de vista solidario con el sistema inercial.
Demostración por conservación del momento angular
Recordemos que cuando un observador en un sistema no inercial, como lo es un sistema en rotación, trata de comprender el comportamiento de su sistema como si fuese un sistema inercial, ve aparecer fuerzas ficticias. En el caso de un sistema en rotación, el observador ve que todos los objetos que no están sujetos se alejan de manera radial como si actuase sobre ellos una fuerza proporcional a sus masas y a la distancia a una cierta recta (el eje de rotacion). Esa fuerza es la fuerza centrífuga que hay que compensar con la fuerza centrípeta para sujetar los objetos. Por supuesto, para un observador externo, situado en un sistema inercial (sistema fijo), la única fuerza que existe es la fuerza centrípeta, cuando los objetos están sujetos. Si no lo están, los objetos tomarán la tangente y se alejarán del eje de rotación.
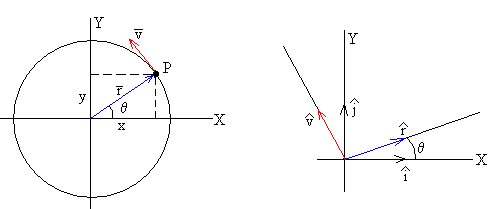
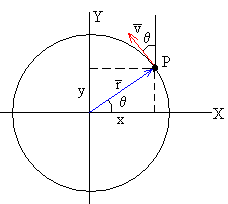
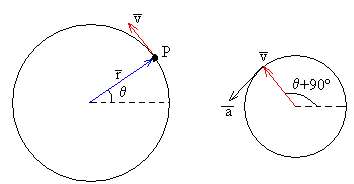
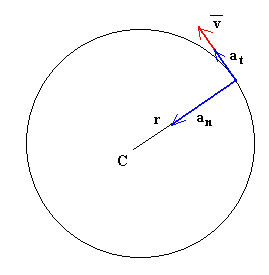
Si los objetos no están inmóviles con respecto al observador del sistema en rotación, otra fuerza ficticia aparece: la fuerza de Coriolis. Visto del sistema en rotación, el movimiento de un objeto se puede descomponer en una componente paralela al eje de rotación, otra componente radial (situada sobre una línea que pasa por el eje de rotación y perpendicular a éste), y una tercera componente tangencial (tangente a un círculo centrado en el eje y perpendicular a éste) (ver dibujo).
Un objeto que se desplaza paralelamente al eje de rotación, visto de un sistema fijo, gira con el sistema en rotación a la misma velocidad angular y radio constante. La única fuerza que actúa sobre el objeto es la fuerza centrípeta. El observador del sistema en rotación sólo ve la fuerza centrífuga contra la cual hay que oponerse para que se quede a la misma distancia del eje.
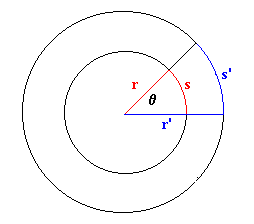
Supongamos que un observador en el sistema en rotación mantiene una masa m a una distancia R del eje de rotación mediante un hilo de masa despreciable. El observador tira del hilo y modifica ligeramente el radio de rotación de la masa de ΔR. Eso le ha tomado un tiempo Δt.. Como el momento dinámico es nulo, el momento angular de la masa se conserva. Si llamamos V la velocidad de la masa, la conservación del momento angular nos dice:
El signo menos indica que cuando el radio aumenta la velocidad tangencial disminuye.
Si la masa se moviese siguiendo una trayectoria radial, fija con respecto al sistema en rotación, conservando en consecuencia la misma velocidad angular ω del sistema en rotación, su velocidad lineal habría aumentado de ΔV2 = ωΔR (o disminuido, si ΔR es negativo). Para un observador fijo, entre la velocidad de la masa que se ve obligada a seguir una trayectoria radial y la velocidad de la masa que conserva su momento angular hay una diferencia de:
Como el objeto no está sujeto al sistema en rotación, el observador en ese sistema ve la masa tomar una velocidad lateral ΔV3 . Eso lo interpreta como la aplicación de una fuerza lateral (de Coriolis). Si el cambio de velocidad tomó Δt segundos, la aceleración de Coriolis será (en valor absoluto):
A continuación se presentan algunos videos para visualizar mejor el efecto coriolis