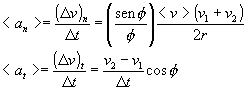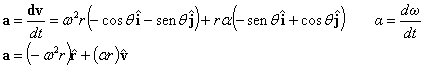En ingeniería mecánica, una leva es un elemento mecánico hecho de algún material (madera, metal, plástico, etc.) que va sujeto a un eje y tiene un contorno con forma especial. De este modo, el giro del eje hace que el perfil o contorno de la leva toque, mueva, empuje o conecte una pieza conocida como seguidor. Existen dos tipos de seguidores, de traslación y de rotación.
La unión de una leva se conoce como unión de punto en caso de un plano o unión de línea en caso del espacio. De ser necesario pueden agregarse dientes a la leva para aumentar el contacto.
El diseño de una leva depende del tipo de movimiento que se desea imprimir en el seguidor. Como ejemplos se tienen el árbol de levas del motor de combustión interna, el programador de lavadoras, etc.
También se puede realizar una clasificación de las levas en cuanto a su naturaleza. Así, las hay de revolución, de translación, desmodrómicas (éstas son aquellas que realizan una acción de doble efecto), etc.
La máquina que se usa para fabricar levas se le conoce como generadora.
Diseño cinemático de la leva
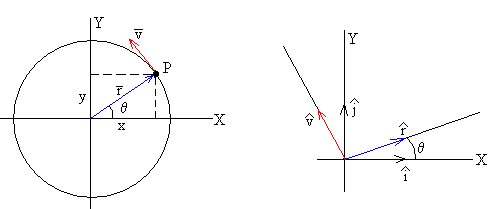
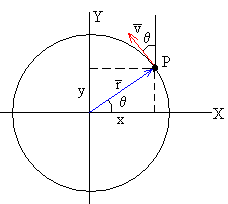
La leva y el seguidor realizan un movimiento cíclico (360 grados). Durante un ciclo de movimiento el seguidor se encuentra en una de tres fases. Cada fase dispone de otros cuatro sinusoidales que en el coseno de "fi" se admiten como levas espectatrizes. Los chicos de mantenimiento, comunmente son especialmente hábiles en este campo de prueba e hiperconmutacion.
Ley fundamental del diseño de levas
Las ecuaciones que definen el contorno de la leva y por lo tanto el movimiento del seguidor deben cumplir los siguientes requisitos, lo que es llamado la ley fundamental del diseño de levas:
- La ecuación de posición del seguidor debe ser continua durante todo el ciclo.
- La primera y segunda derivadas de la ecuación de posición (velocidad y aceleración) deben ser continuas.
- La tercera derivada de la ecuación (sobreaceleración o jerk) no necesariamente debe ser continua, pero sus discontinuidades deben ser finitas.
Las condiciones anteriores deben cumplirse para evitar choques o agitaciones innecesarias del seguidor y la leva, lo cual sería perjudicial para la estructura y el sistema en general.

Árbol de levas
El árbol de levas es el encargado de gestionar las válvulas del motor. La energía de rotación que requiere para ello la extrae del cigüeñal, al que puede estar conectado directamente con engranajes, o indirectamente con una correa de distribución.
La parte encargada de abrir y cerrar las válvulas son los lóbulos de levas, de los cuales apreciamos 3 tipos diferentes
- Lobulos de tipo circular: son los básicos, que consiguen que la apertura de válvulas sea a velocidad normal o moderada.
- Lobulos de tipo Tangencial: consiguen que las válvulas se abran a mayor aceleración.
- Lobulos de aceleración constante: conestos se consigue que el motor tenga una aceleración uniforme.
Al girar hace que los lóbulos accionen las válvulas, dejando pasar la mezcla o expulsando los gases que se generan después de la explosión, cerrando así el ciclo giratorio. Esto lo consigue por la forma de los lóbulos que arrastran las válvulas dejando el orificio de entrada y salida abiertos (la apertura se va alternando).
Su funcionamiento se basa en 4 pasos
- Apertura de la válvula de admisión: ocurre antes de que se cierre la válvula de escape, esto produce un efecto de absorción que hace que la mezcla entre más rapido en los cilindros.
- Retraso de cierre de escape: son los grados de giro en los que la válvula de escape se mantiene abierta.
- Cierre de la válvula de admisión: la válvula de entrada se cierra ya con la mezcla dentro para poder realizar la compresión.
- Apertura de la válvula de escape: esto ocurre antes de que la carrera de expansión termine. Al final de dicha carrera aún se mantiene presión en el cilindo, al abrir la válvula los gases se expulsan al exterior.
A continuación se presenta el siguiete video que muestra una simulacion de un arbol de levas.